Batch 3 - Class 175 - Tiling

• (Dudeney - 368) A man had a ten-gallon keg full of wine and a jug. One day he drew off a jugfull of wine and filled the keg with water. Later on, when the wine and water had got thoroughly mixed, he drew off another jugful and again filled up the keg with water. It was then found that the keg contained equal proportions of wine and water. What was the capacity of the jug?
• Answer: 2.93 gallons

• Can you tile a plane with congruent regular polygons (tiling means that there should be no empty space left)
• Try it with triangles
• Try it with rectangles
• Try it with pentagons
• Try it with hexagons
• How about larger-side polygons. Can you find all polygons that can be tiled?
• Interior angle of a polygon with n sides is 180(n-2)/n. If k of these polygons meet at a point, then total angle k*180(n-2)/n=360. This means that 4/(n-2) should be integral. Thus n could be 3,4 or 6
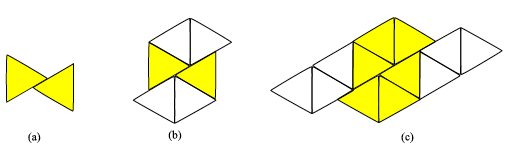
• Is this the only kind of polygon? One can also make a polygon where corners don't meet at all. Now the corner of a polygons must rest along side of the neighboring polygon. The side takes up 180 degrees. So k*180(n-2)/n=180. This leads to n as 3 or 4. Can you figure out such tiling patterns?

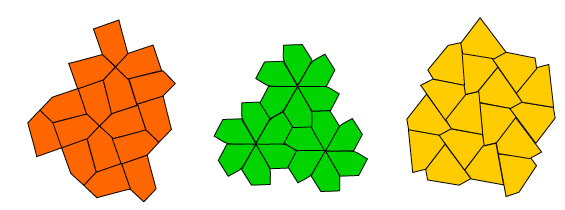
• If we drop the constraint of "regular", can you tile using other polygons? Can you figure out a tiling with irregular pentagon for example?

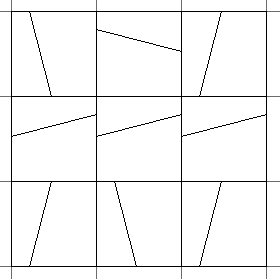
• Or, lets try and draw a tiling with irregular quadrilaterals? Can you take the regular square tiling and convert it into an irregular tiling with different sized quadrilaterals. See Penrose tiling below

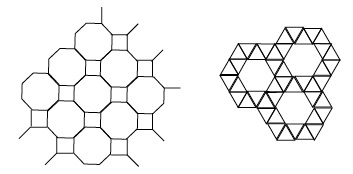
• If we take two different kind of regular polygons, can we tile the plane with more shapes? For example, can you tile using same size regular octagons, and another size regular squares? Hexagon and triangles?

• Non-periodic tiling. Can you 4 congruent sphinx to make a larger similar sphinx? What is the implication in terms of tiling - can you now use this approach to tile?

• Another non-periodic tiling - Spiral tiling (Heinz Voderberg)

• Four towns at four corners of a square. how should they be connected to minimize length of railroad (hint: not diagonally - Its 1+sqrt(3) - essentially two three pointed stars with center of towns as meeting point - 120 degree at star) - interesting demonstration https://www.youtube.com/watch?v=dAyDi1aa40E - Steiner points (but they break down due to local minima)